Hi, welcome to the first post on my dev blog, where I talk about coding, software and a dash of everything else. Since this is my first post, I’ll kick it off by speaking about a project I worked on last year called Eve Subsystem Analysis. It’s a website I made to make mass producing subsystems in Eve Online effortless. In particular, I’d like to talk about how it optimised reaction scheduling to maximise my ISK / hour ratio.

In case that last part didn’t make any sense, Eve Online is an MMORPG from 2004 developed by an Icelandic company called CCP Games. Unlike most MMOs from that period it still has a niche, but vitamin D deficient playerbase. Eve is famous amongst gamers for its complex mechanics and stories of player-driven drama and betrayal. But, beneath the surface is an impressively realised virtual economy where players earn ISK, the fictional in-game currency, by performing various activities from mining, shooting NPCs, trading, or manufacturing.

Spreadsheets in Space

Anyway, I built this website to calculate how many base materials I would need given a certain number of end products. It handles all of the in-game calculations based on the user’s requirements, and spits out the number of raw materials needed.

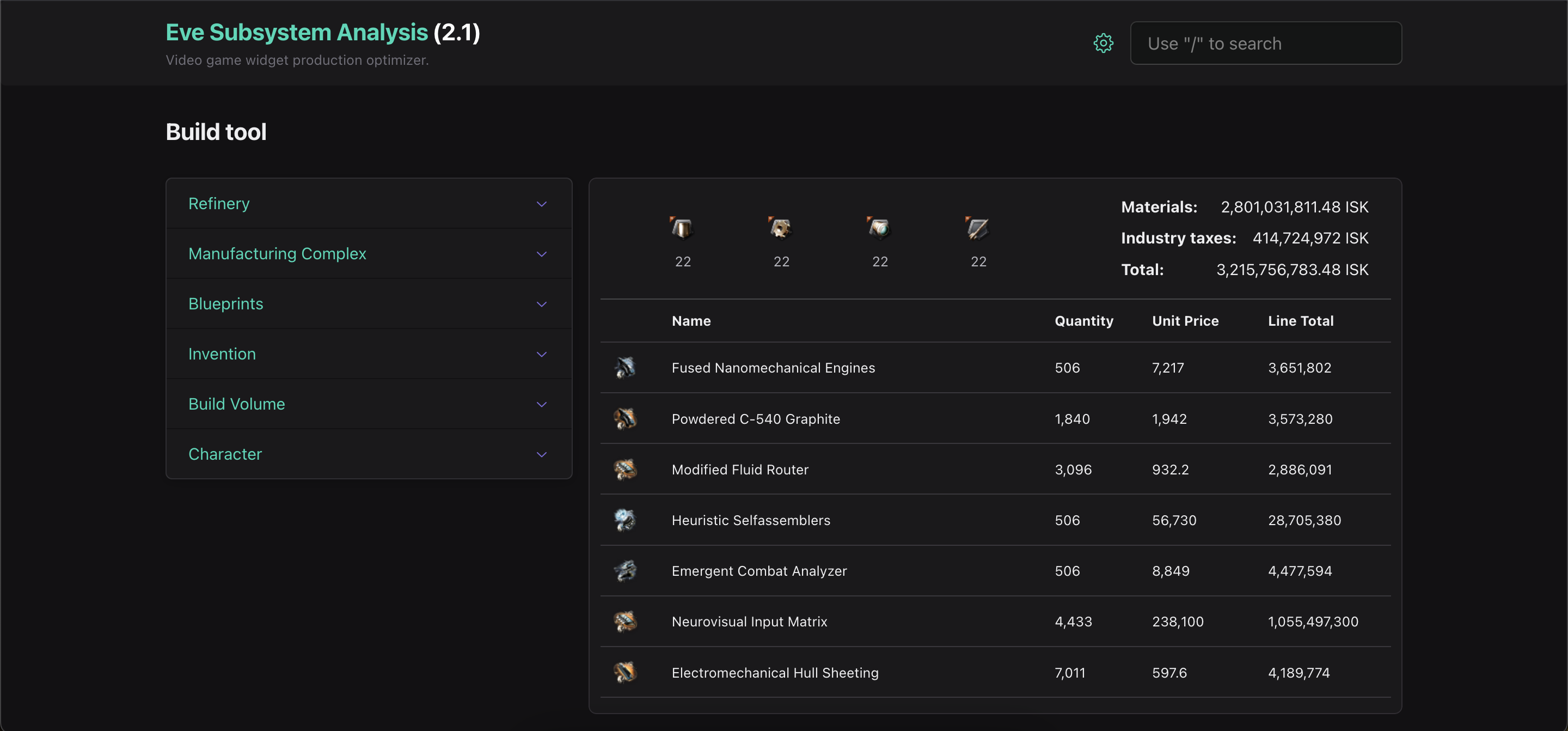
This is not unique. Eve has a thriving third-party developer scene, and there are some really amazing fan-made apps out there, some of which also handle material calculation. What is unique about my app, and what we’re here to talk about today, is reaction scheduling.

The Problem

Reactions are a specific step in the manufacturing process of a lot of items in Eve. This is where you mix up some fuel, gas and minerals to create a new material inside of a special type of player-owned station called a refinery. What this means in practice is a player will have this list of reactions that they have to complete and they’ll have a set number of slots that they can do them in (this is a trainable player skill, up to a max of 11 per character). For subsystems, each reaction takes the same amount of time to execute, but the number of runs per reaction can vary. Also, since users have to log in to begin a reaction, it’s preferable to schedule them in a way that you don’t have to re-use the same slot for two different kinds of reaction when you’re producing, so ideally it’s one type of reaction per slot.

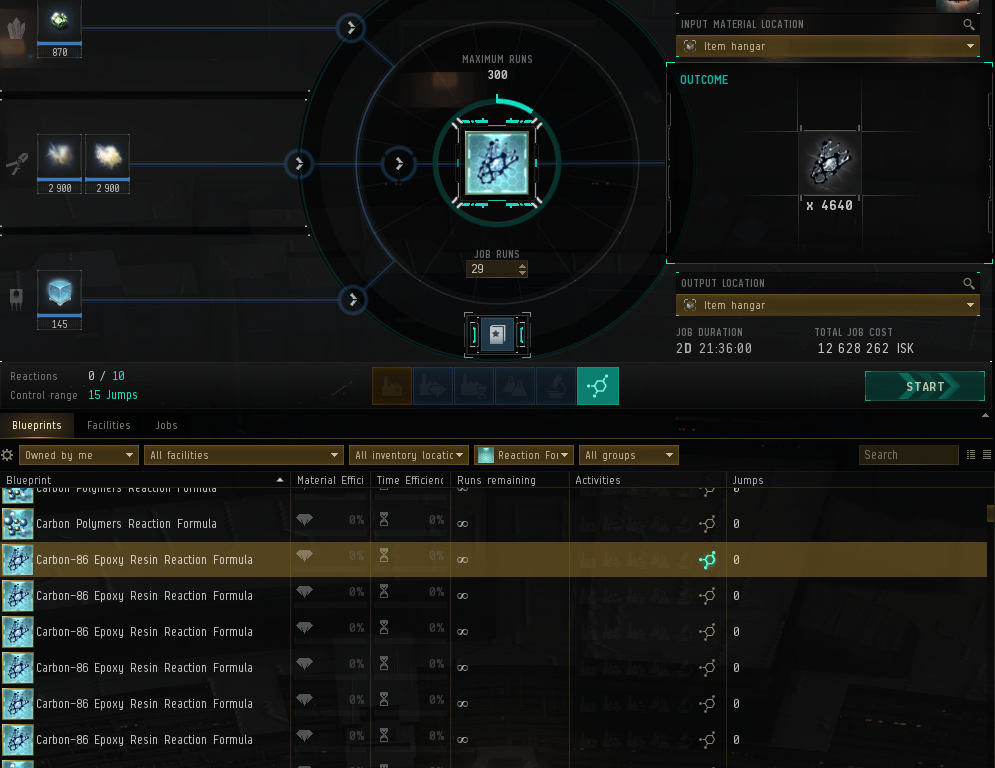
Most people kind of schedule their reactions by vibes, I would guess. You take a number that’s close to the number of reactions total / the number of slots you’ve got, and add a few more in some slots and a few less in others. This achieves the objective of completing all the reactions but it’s not necessarily optimal, and it often leads to having to run reactions for longer than is necessary. I knew that there had to be some way to provide my users with a reaction schedule that both allowed them to run all of their reactions, and distributed those reactions such that they’d be completed in the least amount of time possible.

Dead Ends

In looking for a solution to this issue, I got lost down many rabbit holes. I learned about Bin-Packing Problems (which I think technically fits this kind of issue, but we also have some other constraints which the wikipedia page at least doesn’t account for), Greedy Algorithms (totally not helpful in this case, but still good to know about), and a bunch of other weird computer science terms in search for an answer to this problem.

Brute Force

Let’s quickly summarise the problem before going on to the solution. You have these reactions that need to be done in order to build your subsystems. You also have x amount of slots in which to do them. Each individual reaction takes y amount of time. You don’t want to run multiple types of reaction in the same slot, and you want to find a way to get all of them done in as little time as possible.

Let’s talk about the obvious solution that comes to mind. Each slot gets the mean, or the number of reactions / slots. For this to work, the quantity of each type of reaction’s runs would have to be divisible by the mean with no remainder. In practice, that is such a fluke that it practically never happens in this context, as I learned from experience - but it does get us on the right track!

My first step after realising that this didn’t work was to try adding a 30% upper limit for how many reactions I could perform in each slot. This worked in some instances but it also sometimes led to lots of empty slots, and inefficiency. If you’re wondering right now, what happened to the reactions that still needed to be done but weren’t added into the full mean + 30% slots, they also got their own slot, so you could get a schedule that looks like this:

• Slot 1: 13 Fulleroferrocene Runs
• Slot 2: 13 Fulleroferrocene Runs
• Slot 3: 4 Fulleroferrocene Runs
• Slot 4: 13 Graphene Nanoribbons Runs
• Slot 5: 6 Graphene Nanoribbons Runs
• etc

This is where I finally found a solution to the problem. I decided I’d loop through all of the reactions that needed to be run, and try adding the average number to its own slot. If the number of an individual reaction is not equally divisible by that number, the remainder gets its own slot too. Then, after running all of the reactions that needed to be done, I would check if the number of slots used in total was less than or equal to the number of slots the player had. If not, I’d try again with the mean +1 and run the same checks. Then again at +2 and so on.

Note that because I’m incrementing up from the number of total reactions / the number of slots (the fastest time theoretically possible) the first reaction schedule I arrive at should be the fastest possible, since we’ve already checked that the faster alternatives couldn’t fill our criteria. As a bonus, I was able to further optimise the code by performing a binary search to arrive at the solution in a lot less time than by simply crunching the numbers (to arrive at a reasonable upper bound for the binary search, we simply increase the increment exponentially until a schedule is found which works, and binary search between that and the last one which didn't).

Schedule Demo

If you’re feeling a bit lost in all of this, or you’re a more visual learner, here’s a demo I created to try to help illustrate the point better. It's using the actual scheduling code from the site with some example values put in place for the reactions and number of slots. Just hit the button and it’ll sort the reactions below. Change the number of slots to see how it handles different scenarios, or slow it down to observe it working step by step.

Summing Up

This little scheduling problem turned out to be way more interesting than I expected, and solving it taught me a lot about optimisation and algorithms. What started as a niche quality-of-life feature for my own use turned into a surprisingly satisfying coding challenge—and one that pushed me to learn real-world computer science concepts like binary search and greedy algorithms along the way. I hope this post has given you a bit of insight into how deceptively deep even the smallest features in an application can be.